Perkalian Matriks: August 2018

Perkalian Matriks 2 x 2

Perkalian dua buah matriks di mana kedua matriks tersebut masing-masing memiliki ukuran 2 x 2 akan menghasilkan matriks dengan ukuran 2 x 2 juga. Proses perkalian matriks ini tidak begitu rumit, hal ini dikarenakan anggota-anggota penyusun matriks dengan ukuran 2 x 2 hanya terdiri atas 4 anggota untuk setiap matriks. Sehingga, perkaliannya dapat dengan mudah dilakukan dengan tingkat kerumitan yang rendah.
Cara mengalikan dua buah matriks adalah mengalikan antar baris dan kolom. Penjelasan perkalian matriks 2 x 2 dalam gambar dapat dilihat seperti berikut.
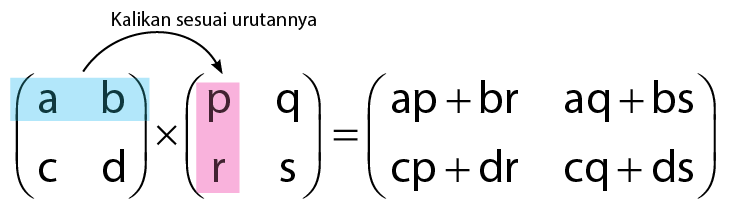
perkalian matriks 2x2

Contoh soal perkalian matriks 2 x 2
Tentukan hasil perkalian matriks A dan B di bawah!

$A = \begin{pmatrix} 3 & 4 \\ 1 & 2 \end{pmatrix}$

$B = \begin{pmatrix} 7 & 5 \\ 6 & 4 \end{pmatrix}$

Jawab:

$A \times B = \begin{pmatrix} 3 & 4 \\ 1 & 2 \end{pmatrix} \times \begin{pmatrix} 7 & 5 \\ 6 & 4 \end{pmatrix}$

$= \begin{pmatrix} 3 \cdot 7 + 4 \cdot 6 & 3 \cdot 5 + 4 \cdot 4 \\ 1 \cdot 7 + 2 \cdot 6 & 1 \cdot 5 + 2 \cdot 4 \end{pmatrix}$

$= \begin{pmatrix} 21 + 24 & 15 + 16 \\ 7 + 12 & 5 + 8 \end{pmatrix}$

$= \begin{pmatrix} 45 & 31 \\ 19 & 13 \end{pmatrix}$

Demikian, proses perkalian matriks antara dua buah matriks dengan ukuran 2 x 2. Mudah bukan? Selanjutnya simak perkalian matriks 3 x 3.

Perkalian Matriks 3 x 3

Perkalian matriks 3 x 3 sedikit lebih rumit dari perkalian matriks 2 x 2. Hal ini dikarenakan ukuran matriks 3 x 3 mempunyai jumlah anggota lebih banyak. Matriks persegi dengan ukuran 3 x 3 memiliki 9 anggota, yang terbagi dalam 3 baris dan 3 kolom. Pada matriks dengan ukuran 3 x 3, setiap baris dan kolom terdiri atas 3 anggota. Konsep perkalian pada matriks dengan ukuran 3 x 3 sama dengan proses perkalian matriks dengan ukuran 2 x 2, hanya saja lebih rumit.

Perhatikan proses perkalian dua buah matriks yang masing-masing berukuran 3 x 3 pada gambar di bawah.

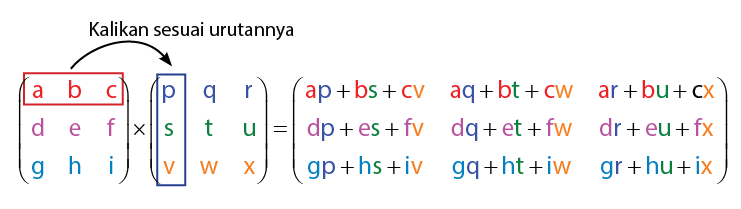
Apakah gambar di atas sudah cukup membuat jelas sobat idschool? Jika belum jelas dapat disimah contoh soal perkalian matriks 3 x 3 berikut untuk menambah pemahaman sobat idschool.
Contoh soal perkalian matriks 3 x 3
Tentukan hasil perkalian matriks 3 x 3 di bawah!

$A = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}$

$B = \begin{pmatrix} 9 & 8 & 7 \\ 6 & 5 & 4 \\ 3 & 2 & 1 \end{pmatrix}$

Jawab:

$A \times B = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix} \times \begin{pmatrix} 9 & 8 & 7 \\ 6 & 5 & 4 \\ 3 & 2 & 1 \end{pmatrix}$

$= \begin{pmatrix} 1 \cdot 9 + 2 \cdot 6 + 3 \cdot 3 & 1 \cdot 8 + 2 \cdot 5 + 3 \cdot 2 & 1 \cdot 7 + 2 \cdot 4 + 3 \cdot 1 \\ 4 \cdot 9 + 5 \cdot 6 + 6 \cdot 3 & 4 \cdot 8 + 5 \cdot 5 + 6 \cdot 2 & 4 \cdot 7 + 5 \cdot 4 + 6 \cdot 1 \\ 7 \cdot 9 + 8 \cdot 6 + 9 \cdot 3 & 7 \cdot 8 + 8 \cdot 5 + 9 \cdot 2 & 7 \cdot 7 + 8 \cdot 4 + 9 \cdot 1 \end{pmatrix}$

$= \begin{pmatrix} 9 + 12 + 9 & 8 + 10 + 6 & 7 + 8 + 3 \\ 36 + 30 + 18 & 32 + 25 + 12 & 28 + 20 + 6 \\ 63 + 48 + 27 & 56 + 40 + 18 & 49 + 32 + 9 \end{pmatrix}$

$= \begin{pmatrix} 30 & 24 & 18 \\ 84 & 69 & 54 \\ 138 & 114 & 90 \end{pmatrix}$

Berikutnya adalah perkalian matriks dengan ukuran yang berbeda. Simak selengkapnya di bawah.

Perkalian Matriks (m x n) x (n x p)

Ulasan terakhir yang akan dibahas melalui halaman ini adalah perkalian dua matriks dengan ukuran berbeda. Konsep perkalian matriks masih sama dengan dua pembahasan sebelumnya, yaitu mengalikan antar elemen-elemen matriks pada baris dan kolom. Sebagai contoh, akan diulas perkalian matriks dengan ukuran 3 x 2 dan matriks dengan ukuran 3 x 2.
Perhatikan proses perkalian dua buah matriks yang masing-masing berukuran (3 x 3) x (3 x 2) pada gambar di bawah.

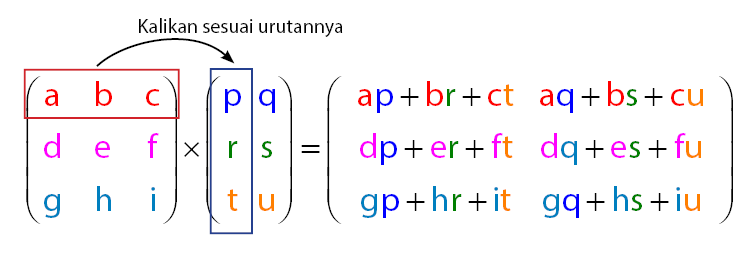
Contoh soal perkalian matriks (3 x 3) x (3 x 2)

$A = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}$

$B = \begin{pmatrix} 6 & 5 \\ 4 & 3 \\ 2 & 1 \end{pmatrix}$

Perkalian Matriks

Tuesday, August 7, 2018

Perkalian Matriks 3 x 3, 2 x 2, dan (m x n) x (n x m)

Perkalian Matriks 2 x 2

Perkalian Matriks 3 x 3

Perkalian Matriks (m x n) x (n x p)